Automatically Generating Wikipedia Artciles: A Structure-Aware Approach (Sauper+, 2009)

• original paper: http://www.aclweb.org/anthology/P09-1024

repo

• github.com/csauper/wikipedia

Goal

タイトルを入れると完全なWikipedia記事を生成する:

"3-M Syndrome" \(\mapsto\) complete article for Wikipedia

感想

• "template-based" とあったから読んでみた
• 思ってたのと違った

Overview

• entity の複数段落の要約 (overview)
  • 原文 (段落) を Yahoo! からたくさん拾ってきて並べる
• + content planning
  • テンプレートとして学習する
• content に最適な文章を
  • perceptron ranking algorithm で学習
  • 整数線形計画法で選択

Content Planning

"Diseases" の content planning の例 (Figure 1):

template = topicの列:

生成物

• Automatically generated Wikipedia articles: people.csail.mit.edu/csauper/?page_id=64
• 例えば
  • 3-M Syndrome: en.wikipedia.org/wiki/3-M_syndrome

生成物

記事のフレーズでググるとまんまの文章が別なページから引っかかる (拾ってきてる)

生成したい文章に必要な文はネットのどこかにあると仮定する. ただし、

1. 複数のページに散らばっている
2. ノイズな文も含まれうる

だから content planning が必要.

Method Overview

1. 前処理
   • 同じドメインの事例からテンプレート (トピックの列) の学習
   • Search: 原文を集める
2. Selection Model: 原文を選ぶ
3. 選んだのを組み合わせる

Method::前処理::訓練事例

訓練データとする文章をネットから集める

• 生成したい記事と近いドメインのもの
• 実験では "Diseases" というドメインの他のWikipedia記事を用いた

文章 \(d_i\) は複数段落 \(s\) ( <p> ) からなり、段落には見出し \(h\) ( <h*> ) がついてる.

事前処理::テンプレート学習 (Section 3.1)

見出しの列

• \(h_1^1 \rightarrow h_1^2 \rightarrow \ldots \rightarrow h_1^m\)
• \(h_2^1 \rightarrow h_2^2 \rightarrow \ldots \rightarrow h_2^m\)
• \(~~~~~~~~~~~\vdots\)

というのを template (topic列) だと見なして、 これを学習したい.

事前処理::テンプレート学習 (Section 3.1)

全見出し \(\{ h_i^j | i, j \}\) をクラスタリング \((t_1, t_2 .. t_k .. )\) して、 一つのクラスタ (多重集合) を topic とする.

• \(t_1 \rightarrow t_3 \rightarrow \ldots \rightarrow t_m\)
• \(t_2 \rightarrow t_3 \rightarrow \ldots \rightarrow t_{m'}\)
• \(~~~~~~~~~~~\vdots\)

みたいな列ができる.

1. この列の長さ \(k\) (平均長) の

majority-order を計算して (majority ordering algorithm [Cohen+, 98] )、 template とする. 1. クラスタ \(t_j\) の要素の最頻の見出し \(h\) をクラスタの見だしとして用いる.

事前処理 (誰か読んで)

• Repeated Bisectioning Algorithm [Zhao+, 05]
  • 文章同士 \((s_i, s_j)\) のコサイン類似度を距離とした階層クラスタリング
• Majority Ordering Algorithm [Cohen+, 98]
  • 有向辺に遷移確率ぽい何かをつけた順序の最適化

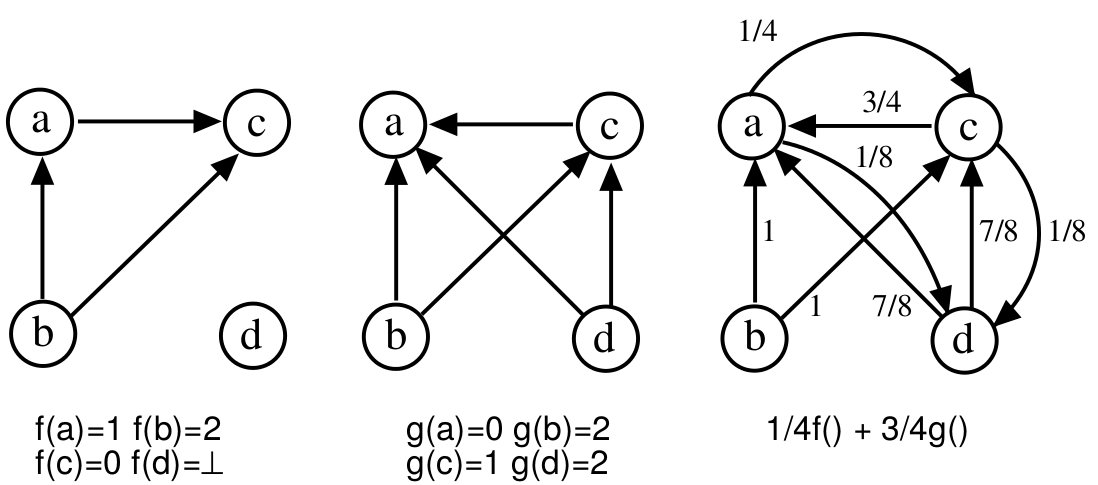
事前処理::Search: 作ったテンプレート毎に excerpts (抜粋) を拾う (Section 3.1)

トピック \(t_j\) 毎に、できるだけたくさん excerpts を拾う

1. "記事タイトル (entity) + 見出し \(h\) ( \(h \in t\) )" で Yahoo! でググる
   • e.g. "3-M Syndrome"+diagnosis
2. 上位10ページ採用
3. 見出しと段落のペアを一つの excerpts として抽出

平均で 6 excerpts/topic 取れた

ここまで

ドメイン (e.g. "Diseases") に対して、 テンプレート \(t_1 ... t_k\) . トピックごとに候補となる抜粋

• \(t_1\) : \(e_{11}, e_{12} ~...~ e_{1r_1}\)
• \(t_2\) : \(e_{21}, e_{22} ~...~ e_{2r_2}\)
• \(~~~~~\vdots\)
• \(t_k\) : \(e_{k1}, e_{k2} ~...~ e_{kr_k}\)

抜粋 を一つずつ選択していくことで、 最終的な記事を生成する. ただし、

1. coverage and redundancy のバランス
2. ノイズを上手く避ける必要

Selection Model (Section 3.2.1)

候補 excerpts から一つずつを選択するモデル

• 入力
  1. 記事タイトル
  2. トピックの列 \((t_1, \ldots, t_k)\)
  3. トピック \(t_j\) に対して候補 \((e_j^k)_{k=1..r}\)
• パラメータ
  1. 素性 \(\phi : e \mapsto \phi(e) \in \mathbb{R}^n\) (天から与えられる)
  2. \(t_j\) に対応する重み \(w_j \in \mathbb{R}^n\) (学習する)

推定と学習

• \(w_j\) の学習: perceptron ranking algorithm
  • ドメイン-トピックに依存した重み
• 推定: 整数線形計画法 (ILP)

推定::Ranking

トピック \(t_j\) に対して、excerpt \(e\) のスコアを

で与える. 候補 \((e_1, e_2, \ldots, e_r)\) を、この score の高い順で並び替える.

( \(e_\ell\) は \(\ell\) 番目に良い).

推定::最適化

ランキングで並び替えした後

• \(t_1\) : \(e_{11}, e_{12} ~...~ e_{1r_1}\)
• \(t_2\) : \(e_{21}, e_{22} ~...~ e_{2r_2}\)
• \(~~~~~\vdots\)
• \(t_k\) : \(e_{k1}, e_{k2} ~...~ e_{kr_k}\)

インディケータ \(x_{j\ell}\) は \(e_{j\ell}\) を選択するとき \(1\) 、さもなくば \(0\) .

制約 (ちょうど一つだけ選択すること):

推定::最適化::Redundancy Constraints

内容の冗長性をできるだけ取り除く為の制約:

を加える.

ここで、 \(sim\) は文章同士の cos 類似度.

推定::最適化::Solving the ILP

• lp_solve は厳密解を与える (NP-hard)
• 近似アルゴリズム: knapsack problem [McDonald, 07]

\(w_j\) の学習

perceptron ranking algorithm に基づく.

Perceptron Ranking Algorithm [Collins, 02] (蛇足)

• Max-Ent によるPOSタグ付け
• 最上位のものを出力する代わりに
  • 上位20を取って re-rank していくビームサーチ
  • 複数の候補から一番良いものを学習する

The perceptron training for ranking

• 入力
  • 答え \(x_1\) , 他の候補 \(x_2, x_3 ~..~ x_k\)
  • 素性 \(\phi: x \mapsto \phi(x) \in \mathbb{R}^s\)
  • スコア \(score(x,w) = w \cdot \phi(x)\)

• 初期化
  • \(w^0 = 0 \in \mathbb{R}^s\)
• For \(i=1,2 ~..~ n\)
  • \(j = \text{argmax}_j ~ score(x_j, w^{i-1})\)
  • If \(j=1\)
    • Then \(w^i = w^{i-1}\)
    • Else \(w^i = w^{i-1} + \phi(x_1) - \phi(x_j)\)

Update

\(score(x_1, w) \lt score(x_j, w) (j\ne 1)\) のとき (Else節)、

を大きくすればよい.

• Else \(w^i = w^{i-1} + \phi(x_1) - \phi(x_j)\)

voted perceptron (もっと蛇足)

学習の経過で作られた \(w^1, w^2 ~..~ w^n\) を全て用いる.

• 入力
  • \(x_1, x_2 ~..~ x_k\)
  • 同じ素性 \(\phi: x \mapsto \phi(x)\)
• 初期化
  • 長さ \(n\) の配列 V[] = [0, 0, .. 0]
• For \(i=1,2,..n\)
  • \(w^i\) で score が最上位の \(j = \text{argmax}_j score(x_j, w^i)\)
  • V[i] += 1
• 出力 \(x_j\) where \(j = \text{argmax}_j V[j]\)

学習::Ranking Perceptron

テンプレートを作る元文章からゴールドデータ \(s_1, s_2 ~..~ s_k\) を正解として用いる.

• \(t_1\) : \(s_1\) ; \(e_{11}, e_{12} ~..~ e_{1r_1}\)
• \(t_2\) : \(s_2\) ; \(e_{21}, e_{22} ~..~ e_{2r_2}\)
• \(\vdots\)
• \(t_k\) : \(s_k\) ; \(e_{k1}, e_{k2} ~..~ e_{kr_k}\)

1. Rank with \(w_j \mapsto (e_{j1} ~..~ e_{jr}) ~ \forall j\)
2. Optimize as a ILP \(x_j = Opt(e_{j1} ~..~ e_{jr}) ~ \forall j\)
3. If \(sim(s_j, x_j) \geq 0.8\)
   • Then \(w_j\) を更新しない
   • Else \(w_j = w_j + \phi(s_j) - \phi(x_j)\)

評価

1. ROUGE-1
   • テストデータ (Wikipedia記事として既にあるもの) を訓練データ (Wikipedia記事)+Yahoo!(該当記事を参照しない) で生成してROUGEで比較
2. REACTIONS
   • 実際にWikipediaに投稿してみんなの反応を見る

データ

• ドメイン:
  • American Film Actors: 2150 articles in Wikipedia
  • Diseases: 523
• 各ドメインの90% の文章を訓練とする.
• 残り10%をテストとする
  • 生成する際は、記事のタイトルだけを参照する
• 平均 4 topic (段落)
• Search 手続き (Yahoo!) 中ではテストデータ自体を参照しないようにする

Baselines

1. Search
   • パーセプトロンでランキングせずに、検索結果で引っかかった順にランク付けを行う
   • 1ページから \(k\) 段落拾ってきた場合には、それをそのまま候補として用いる
   • 大抵、ページの一番初めの段落は comprehensive overview であるので summary としては優秀
2. NoTemplate
   • テンプレート (トピック列) を気にしない
   • Search では、記事のタイトルだけで検索する (full model では記事タイトル+見出し)
   • 文の組合せ方は既存手法に従う [Zhou 04; Biadsy 08]
3. Disjoint
   • ILPを行わない
   • ランキングの後、各トピックから1位のものだけを選択して組み合わせる
4. Oracle
   • 候補からテストデータとコサイン類似度が高いものを選択する
   • 生成すべきテストデータを参照する上にROUGEで評価するので
   • ランキングアルゴリズムに関する精度の上限を与えると考える

ROUGE-1 結果 (Table 3)

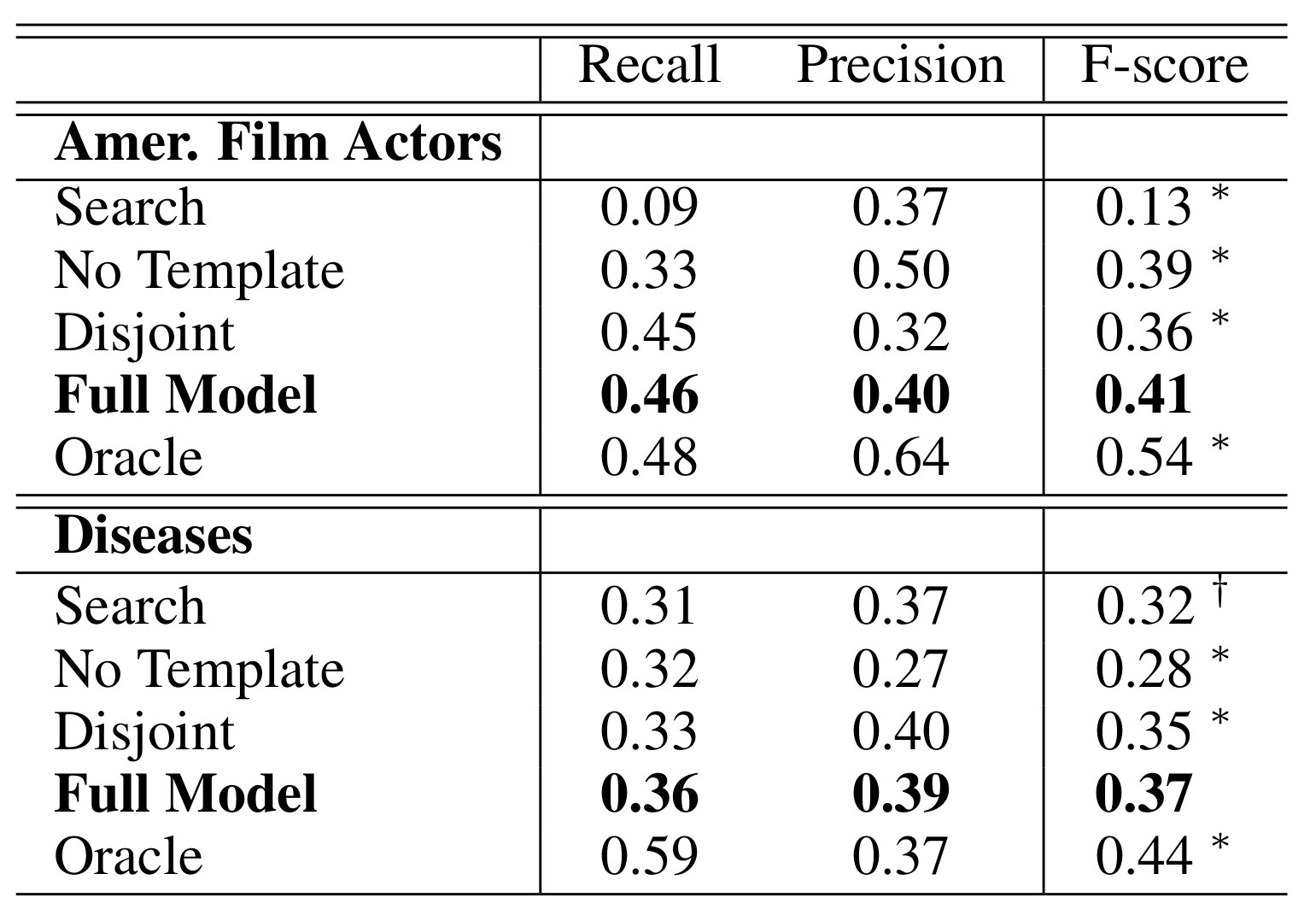
• Oracle は上限
• No Template は一つのトピックに集中してしまう
• FullModel と Disjoint との差がランキングの良さ
• Search はまちまち. 良い記事を引けば良い

REACTIONS

15の記事を投稿、5-11ヶ月放置

• 10 promoted from stubs to regular entries
• 全ての記事が人手で編集された
• 削除がなされた記事は無い
• 記事中の三箇所 (1 section + 2 smaller pieces) が削除された

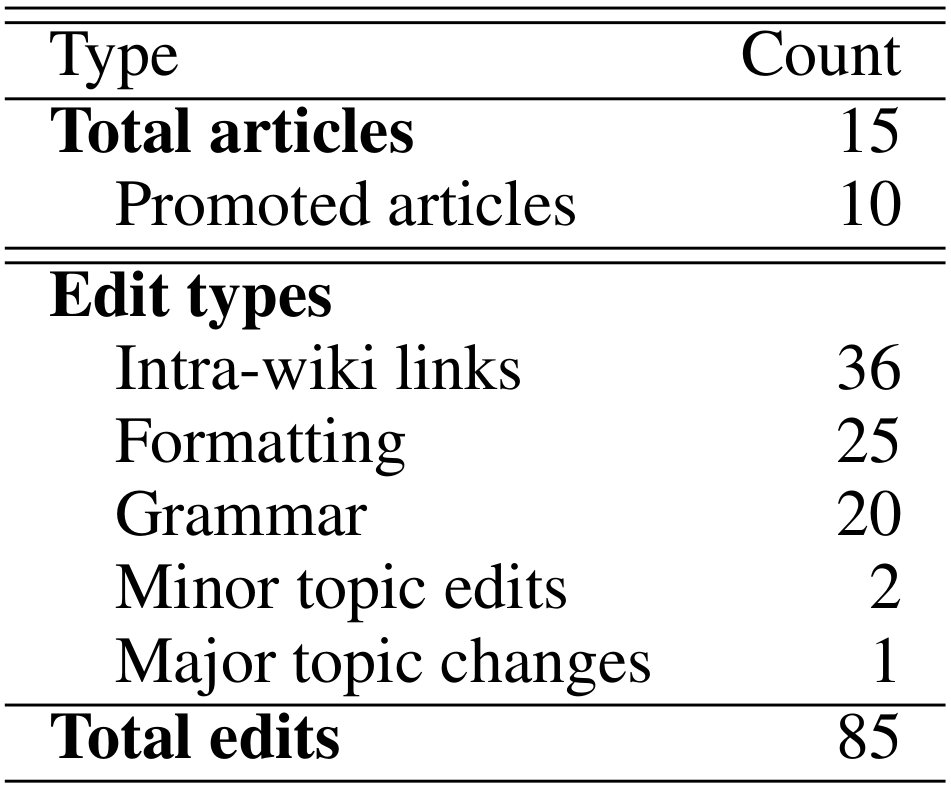
• The most common changes were small edits to formatting and introduction of links to other Wikipedia articles