月報 2022/08

Tue 02 Aug 2022

00:12:20

残念ながら私の忘れっぽさの為に毎日とは言わないが, それでもほとんど毎日, 寝る前にヤクルト1000を飲むようにしている. 効果は間違いなく体験してるので心配しないでください.

15:06:26

• neovim の中の ranger がおかしい [2022/08/02 (Tue) 15:30]
  • ファイルを選ぶと ranger の中で開いてしまって neovim で開かない
    • システム上の Python をそういえばこないだアップグレードしたから必要な依存ライブラリを入れ直す必要があった
• zellij をもう一回試す
• 重たい git ディレクトリにいると zsh が重たい [2022/08/02 (Tue) 15:16]
  • プロンプトで git コマンドを叩いてるからだよ

15:57:01

やりたいこと. 点字の習得, 目隠しルービックキューブの習得. 点字について. やはり見て覚えるというのは無理だ. 受験生のときに英単語をどう覚えていたかといえば一つはノートに例文をひたすら書き連ねることだが, これは手が痛くなるし, 紙と鉛筆を消費してもったいないし, 効率が悪い. 思い出すに, ひたすらパソコンでタイピングをしてた覚えがある. というわけで点字もタイピングで習得しよう.

PC のブラウザで動く.

19:28:23

風の噂の「風」は知った風を言うの「風」

洗濯機を修理してもらった. 前調べしてたように（"ビッグドラム F19" で調べてすぐに分かっていた事だが）やはりファンの交換になった. 部品代が1560円, 技術料が11200円, 出張料が3500円. 高い. 技術料なんていうけど蓋開けてネジ外して交換するだけに一万円の技術があるわけではなく, メーカー正規の部品を手に入れる権利に一万円の価値があるというだけに過ぎない. これらは事前の説明があったからいいけど, パーキング代金として330円取られたのは笑ってしまった. つまり, おっさんがトラックか何か車で来て近所のコインパーキングで停めたからそのお金を私に請求するらしい. これがガソリン代の請求だったら困るけど, 330円くらいならと思っていちいち騒ぐ気にもならなかった. （騒いだところで, パーキング代はオマケしてやる, その代わりに技術料を330円増やすねってなるだけじゃん.） 一度, 日立製品を買ってしまったらもう消費者は日立というメーカーに従うことしかできない. （特定のメーカーを悪く言いたいわけではなくてどこで買おうが結局同じことだと思う.）

Wed 03 Aug 2022

20:25:02

zellij に改めて入門する. zellij はなんと発音すればよいだろう. アラビア語らしい.

21:23:57

やっぱり要らないわこれ

Thu 04 Aug 2022

11:03:00

点字方式タイプライター、マジでアリだと思うな。 ステノタイプ、ステノワードがこれに近そう、という指摘。

やはり、やることは同じで、キー数を減らして、同時押しの組み合わせで表現しようとしている。 同時押しというのは我々が普段使うキーボードだとせいぜい Ctrl や Shift といった「装飾」に関する同時押しをする程度だが、完全に任意の組み合わせでの同時押しを要求する。

点字方式では6点のものを想定していた。 この各点を6つのキーに割当て、それらを同時押しさせようというものである。 6つならホームポジションに置くことができるので便利な一方で、指をフルに活用していないという考えもある。

調べると、8点式の点字というのもあるらしい。 漢字の為の漢点字というものらしい。

昨日からSKKの練習をしてる。入力が遅くなったのでイライラしてる。 入力速度が落ちると結果的に文体も変わる気がする。 あと、句読点の設定方法が分からず「、。」を素直に使ってる。

Fri 05 Aug 2022

11:59:55

ルンバは30分くらいで仕事を終えるときと, 90分たった今でも終えないときとがある.

23:00:08

ルール42：どうせ面白いと分かってるアニメは見なくても良い

Sun 07 Aug 2022

21:07:45

アキバヨドバシで電気シェーバー買ってきた. 高かった. 保証は5年で保証書は最初の化粧箱の中に入ってる. 替えの洗浄機は洗濯機上の棚の中にある.

22:15:58

T字の安全カミソリしか使ったことがなかったんだが, これを見てさっさと電気シェーバに切り替えないなと思った次第

お風呂で時間を掛けてカミソリで剃ってると肌は乾燥するし血は出まくるのは, 自分の肌が弱いせいだと思ってたけど, 皆そうなるものらしい.

Wed 10 Aug 2022

23:04:47

3x3x3 ルービックキューブソルバー書いてる

キューブの状態とゴールの状態を指定して, 解くアルゴリズムを探索する. 幅優先で双方向探索をするので最短なものから順に提示する. 探索に使う回転操作はユーザーがオプションで指定する. 例えば -F は F と F' を探索に使うことを意味する. -FUR が大体右手で普通に回しやすい. この3つで解けるとは限らないので, そしたら -FURM にしてみたり -FURr にしてみたりする. M' は回しやすいんだけど M は回しにくいね. 今のところは -M としたらその2つどちらも使ってしまう.

J-perm (a) のアルゴリズムを調べるとほとんどどの資料を見ても L が入っててやや回しにくい. L は意味としては r ( Rw ) と同じはずだから, これを代わりに使うことでどうにかなるはずだ.

cube では cube/ja at main · cympfh/cube · GitHub こんなテキストファイルを用意して標準入力に与える.

$ cube -FURr -n 3 < tests/pll/ja

これで FURr という4つの回転操作だけを使ってアルゴリズムを探索する. 3つ見付けた時点で探索を終了する.

こんなアルゴリズムを見付けた.

\[r_2FrU_2 - R'FRU - F'r'\]

私が知る限りこのアルゴリズムを紹介してる資料は無い. 最後の \(F'r'\) だけやや持ち替えを要するので苦しい. しかしその手前は \(R'FRU\) のリズムが二回繰り返されているので気持ち良い.

Sun 14 Aug 2022

00:00:18

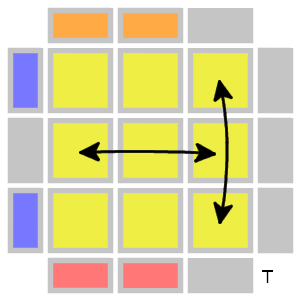
ルービックキューブの一面を図示するだけのツールを書いた.

インターネットにはたくさん解説サイトがあって, サイトごとにきれいな図が置いてあるわけだが, あれはみんなどうやって作ってるのかな. 少し調べたけど作図ツールみたいなものは見当たらなかった. 有名なのがあるとしたら皆同じような図を使ってるはずだが, そうなっていないということは有名なツールというものは無いことを示唆してる. しょうがないので作るしか無い.

上の cubeviz は偉そうな名前の割にまだ一面を図示することしかできない.

これを使って, 画像を差し替えた. ただし矢印は上のツールでは表示できないので, GIMP で矢印を書き込む等した.

00:04:34

色の指定とかサイズの指定とか, オプションで出来るべきことを一切してない.

01:47:34

ツール無いって言ったけど全然ありそうだな.

imagecube.php

これは F2L の説明に良さそう.

RubikNotes

これもいい. アルゴリズムから画像を作ってくれる機能が良い.

でも出力画像の見た目は私のが一番キレイだな.

22:41:01

N-perm いいものを探す

今知ってるのは,

• N-perm (a):
  • (RU'L U2 R'UL')2
• N-perm (b):
  • 上の鏡手順

RもLも使うので回しやすくはない. L を使わない手順を探す. 問題は上に示したものは 16 手でここに AUF があるので, PPL の中でダントツに手数が長くて探索が大変.

上に示したアルゴリズムが (X)2 の形をしてるのを真似して, その形式のアルゴリズムで探すことにする.

• N-perm (a):
  1. (RU'r B2 R'Br')2
  2. x' - (RF'r U2 R'Ur')2 - x
     • B を嫌うならこの持ち替えかなあ
  3. 下の (b) の鏡手順. いっそこれもアリか?
     • (lF'l F2 l'U2L')2
• N-perm (b)
  1. (r'FR' F2 rU'R)2
     • 3つ目の R' が回しにくくなければそれ以外は良さそう

見ての通り基本的には L を無理矢理 r に書き直しただけで, 本質的に新しいアルゴリズムではない.

一旦 2. 4. を採用して練習してみる

Tue 16 Aug 2022

13:53:35

昨日から各ECサイトでのクレジットカード決済が通りにくくなった. 試したのは eplus, eeo, dlsite. 怪しいことに何度もトライすると一回上手く行く. eeo に関しては Amazon Pay で払えることに気づいたのでそうした. ありがたい. PayPal, Amazon Pay が一番好きなナンタラPayです. dlsite に関してはちょうど 3Dセキュア2.0 に切り替える直前だったらしい（？）, がまだ切り替える前の話だしそれが今関係するのかは知らない. それが何なのかも知らない.

19:46:39

昨日から「銃・病原菌・鉄」を読み始めた. 勝手に「層・圏・トポス」といった単語を３つ並べる形式の初出だと思っていたし, だから相当古い本なんだと思ってたけど, 初出は 1998年 とかなり最近だった. 自分が生まれて以前以後で考えてるので 1998 は最近だ. 今読んでる草思社文庫はなんと初刷が 2012年だからこれは本当に最近.

見えるところにある島には渡ろうという意志

22:35:47

grow.md が壊れてたので直した. 原因は FastAPI の StaticFiles の仕様が変わってた. 404 な状態を返すのに Response オブジェクトで返す場合と Error 例外で返す場合とが混ざった状態になっている. 昔は前者だけだったのが, 今は両方ありえる！ 「404 だったらここにリダイレクトする」という処理を StaticFiles のオーバーライドすることで実現してたのだが, ここを try catch に書き換える必要が生じていた.

調べる:

• 長周新聞
• 所感派/国際派
• 日本共産党左派

Wed 17 Aug 2022

12:31:07

しっぺ返し戦略は日常生活でも必要な技術.

Fri 19 Aug 2022

18:42:44

攻殻機動隊 sac_2045 の Part 2, 賭双 を見た. ので Netflix を解約した.

好きな漫画がアニメ化しても, もういちいち真面目に見なくても良いかという気持ちが強い. マス対コアという感じ.

Sun 21 Aug 2022

19:50:53

今朝の夢日記。ホームセンターだかペットショップみたいなところを歩いてる。 小鳥のコーナーを覗くことにした。餌などが並んでる棚を見ると商品の隙間に一匹の白文鳥がいた。 どうやら逃げ出したらしい。私と目が合うと店内と飛び回って、でもすぐに戻ってきた。 お店より外に逃げ出すつもりはないらしい。十分に人馴れしてるようで、私がちっちっと呼ぶと私の手の上に乗ったり肩に乗る。 私はそのまま自分の家まで連れてきた。名前を文2とした。 すでに家に飼ってる文鳥に鳥かご越しに合わせた。

Mon 22 Aug 2022

Thu 25 Aug 2022

13:09:07

\(RU' LU - R'U' L'U\)

Sat 27 Aug 2022

00:15:16

• Direct: 590 Mbps
• JP: 200 Mbps, 310 Mbps
• HK: 72 Mbps, 82 Mbps
• Singapore: 810 Kbps
• Vietnam: NA

Sun 28 Aug 2022

夢日記。中学卒業が取り消しになったのでその資格のために中学をやり直しになった。 これを卒業したら高校大学はどうするのだろうと不安になる。

21:08:52

• nintendo online 解約
• GeoGuessr 解約

Mon 29 Aug 2022

11:54:22

昨日の夢日記を書いた. 受験や学校をやり直す夢, 未だに何度も見てしまう. そこまで恐怖の対象だと思ってるんだろうか.

紙Twitterのノートが半分以上埋まってきた. インターネットよりログが貯まるのが速い.

13:51:53

それはそうとしても, vim の暗号化機能相当が neovim でも使いたいという気持ちはある.

neovim からは意図的に取り除かれていて, セキュリティを担保して上手に実装する方法があるなら採用する余地を残しているそう. というのも vim のそれはセキュリティ面にまだまだ不安がある.

Vim でテキストファイルを簡易的に暗号化できると便利な面があるかもしれないと考えた

私も便利に使ってる一人なので. 別にエディタの標準機能にある必要はなくて, gpg で暗号化/復号化が出来て, エディタで開く際に復号化して保存の際に暗号化してくれるプラグインがあればいいんだよな.

18:50:32

t-SNE は使い物にならない. "Local Ordinal Embeddings" ( http://www.tml.cs.uni-tuebingen.de/team/luxburg/publications/TeradaLuxburg_ICML2014.pdf ) を読む.

今日のインターネット

現代のラッダイト運動はTwitter でクソミソに叩くこと. AI によって自分たちの職業, 表現方法が奪われる, 盗まれると思う人たちの行為.

18:54:07

最近は3つSNSをやってて, Twitter と journal.vim と紙Twitterをやってる. 近くにペンとノートがあれば紙Twitterで, 目の前にPCがあって特にリアルタイムに人に言うことでなければ journal.vim で, スマホしかなければ Twitter になる. これらは特に集約されません. 一年後にも残るのは journal.vim だけです. これは適切にプライバシーに関わる箇所を黒塗りした上で月報として公開しています.

Tue 30 Aug 2022

00:54:16

Majorization Algorithm, 優関数法. この「優関数法」という対訳は ざっくりとMajorization techniqueを解説(参考: Modern Multidimensional Scaling) - Qiita でしか目撃しないけど, 一般的なのかな. 優れるとかいう形容詞を使うのは良くないと思うんだけどな.

目的関数を \(f(x)\) とする最小化問題を考える. ここで \(f \colon X \to \mathbb R\) . 補助関数として \(g \colon X \times X \to \mathbb R\) というものを考える. ただし次の2つを満たすものとする.

• \(g(x,x) = f(x)\)
• \(g(x,y) \geq f(x)\)

このとき \(g\) のことを \(f\) の majorization 関数と呼ぶ.

今 \(g(x,x)\) よりも \(g(x',x)\) のほうが真に小さいとする. すると次の不等号式が得られる.

\[f(x') \leq g(x',x) \lt g(x,x) = f(x)\]

このことから次のことが言える.

\(x\) が与えられたときに \(g(x',x) \lt g(x,x)\) なるような \(x'\) を見つけてくる操作があるとする. この操作を適当な \(x\) に繰り返し適用することで, \(f\) の値をいくらでも小さくできる.

これだけなので厳密に収束値が最適解（最小値）だとは限らない気がするけど, \(g\) に関して最適解なら \(f\) も最適だとは言って良さそう.

直接 \(f\) を最適化するのは難しいが, 簡単な形の \(g\) を構成してこれれば, そっちを最適化することで元の \(f\) も自動的に最適化されるというテクニック.

この手法の初出を知らないんだけど, 大体みんな距離学習の文脈で使ってる. 初出を辿ろうとしたけど Groenen, "Multidimensional scaling of interval dissimilarities" の論文まで辿って, この論文が読めないのでここで途切れた.

\(f\) に対して自明な majorization function として次のものがある. ただし \(f \colon \mathbb R \to \mathbb R\) だとしちゃう.

\[g(x,y) = f(x) + (x-y)^2\]

これは簡単すぎるし, 別に便利ではない. このような \(g\) が最適化できるなら \(f\) の最適化も簡単なはずだ. まあでも Majorization Algorithm が一体何をやってるのかをこれを使って調べる.

\(x\) が与えられたときに \(\mathrm{argmin}_{x'} g(x', x)\) を求めたい. これは第一引数で偏微分してそれがゼロという方程式を解けば良くて,

\[\partial_x g(x,y) = \partial_x f(x) + 2x - 2y = 0\]

なので

\[\frac{1}{2} \partial_x f(x') + x' = x\]

なる \(x'\) を持ってくれば良い. 左辺に \(f\) の微分が入ってる時点でよく分からんね.

\(\partial_x\) は \(d/dx\) の偏微分です.

これ誤魔化して, \(x\) と \(x'\) は近いだろうと勝手に仮定して, \(\partial_x f(x')\) を \(\partial_x f(x)\) で近似してみようか. そうしたら

\[x' = x - \frac{1}{2} \partial_x f(x)\]

となる. ただの勾配法になった.

• 適当な \(x\) を与える
• 次を収束するまで繰り返す
  • \(x \leftarrow x - \frac{1}{2} \partial_x f(x)\)

元の \(\frac{1}{2} \partial_x f(x') + x' = x\) に戻る.

• \(f=1\) , \(x' = x\)
  • 最初の \(x\) から動かない
• \(f=x\) , \(x' = x - 1/2\)
  • 無限に小さくなる
• \(f=x^2\) , \(x' = x/2\)
  • ゼロに収束
• \(f=x^3\) , 根が2つ
  • 正の根を使えばゼロに収束

簡単な多項式でしかそもそも陽に解けないな.

18:18:40

多義性を考慮して多重ベクトルをもたせた推薦システム #idea